RankIQA-论文笔记

RankIQA


        RankIQA是2017年的一篇应用于无参考图像质量评价领域的优秀论文，它发表于当年的ICCV。文章创新性地将Siamese网络的相关思想应用于图像质量评价模型的预训练中，并提出了一系列用于预训练IQA模型以及优化Siamese网络的实用方法。读完之后受益颇深，且引发了进一步思考。本文接下来将结合原论文并根据自身理解详细介绍RankIQA图像质量评价模型的训练全过程。

主要思想：

        近些年来由于深度神经网络在图像数据处理的各个领域均取得了显著成效获得可观成果，因此越来越多的学者开始尝试将深度神经网络应用于图像质量评价，但与其他图像处理识别任务不同，对图像质量的评定带有很强的主观因素且需要评定者有很强的专业素养，因此大多数的图像质量评价数据集均由相关专业的群体包含几百的专业人士根据给定的参考图像进行打分，这是一件十分耗费人力的工作同时也导致数据集的构建成本十分高昂，因此目前图像质量评价领域的相关数据集均为小型数据集，将其直接用于特大深度神经网络模型的训练极易引发过拟合，无法真正地表达出其他图像的质量水平。因此作者受到启发，虽然标注有明确质量信息的相关数据很难获得但通过给图像添加干扰获得一系列的受损图像却可以根据添加的干扰多少对其进行排序，通过这种排序好的数据集进行预训练就可以解决目前状态下质量评价数据集缺少的问题。
        首先本文中作者预训练时使用的Siamese网络为共享权重的孪生神经网络，在实际代码中用于对比的两个失真图像实际上也是经过同一个网络进行正向传播获得输出并进行对比的，对于文中的Siamese网络而言它的两个分支完全相同且属于一个图像将获得一个对应的标量输出，这一标量就表示了模型对于输入图像质量分数的预测，在预训练阶段标注信息是图像的质量排名，而Siamese网络也将对比这一标量并对模型进行优化，而在最后的微调阶段这一标量将用于拟合图像的质量分数标注，并通过MSE损失计算相关误差。本文接下来的内容将详细介绍预训练阶段Siamese网络的训练实现。

Hinge Loss（折页损失函数，铰链损失）

        根据坐着的介绍，RankIQA的预训练任务目标是根据图像质量对图像进行排序因此引入了pairwise ranking hinge loss（图像对之间的铰链损失函数）：
        为了更好地理解上述公式的含义本文接下来一段的内容将简单介绍一下Hinge Loss。Hinge Loss是机器学习领域中的一种损失函数，其最著名的应用是作为SVM在二分类情况下，公式如下：

L(y) = max(0 , 1 – t⋅y)

其中，y是预测值(-1到1之间)，t为目标值(1或 -1)。其含义为，y的值在 -1到1之间即可，并不鼓励 |y|>1，即让某个样本能够正确分类就可以了，不鼓励分类器过度自信，当样本与分割线的距离超过1时并不会有任何奖励。目的在于使分类器更专注于整体的分类误差。在实际应用中，一方面，预测值y并不总是属于[-1,1]，也可能属于其他的取值范围；另一方面，很多时候我们希望训练的是两个元素之间的相似关系，而非样本的类别得分。所以下面的公式可能会更加常用：

L( y, y′) = max( 0, margin – (y–y′) )

= max( 0, margin + (y′–y) )

= max( 0, margin + y′ – y)

其中，y是正确预测的得分，y′是错误预测的得分，两者的差值可用来表示两种预测结果的相似关系，margin是一个由自己指定的安全系数。我们希望正确预测的得分高于错误预测的得分，且高出一个边界值 margin，换句话说，y越高越好，y′ 越低越好，(y–y′)越大越好，(y′–y)越小越好，但二者得分之差最多为margin就足够了，差距更大并不会有任何奖励。这样设计的目的在于，对单个样本正确分类只要有margin的把握就足够了，更大的把握则不必要，过分注重单个样本的分类效果反而有可能使整体的分类效果变坏。分类器应该更加专注于整体的分类误差。

举个栗子，假设有3个类cat、car、frog：

img

第一列表示样本真实类别为cat，分类器判断样本为cat的分数为3.2，判断为car的分数为5.1，判断为frog的分数为 -1.7。那这里的 hinge loss 怎么计算呢？

这里是让其他两类的分数去减去真实类别的分数，这相当于计算其他类与真实类之间的误差。因为我们希望错误类别的评分低于正确类别的评分，所以这个误差值越小越好。另外，还使用了一个边界值margin，取值为1，为了使训练出的分类器有更大的把握进行正确分类。

有多种 hinge loss 的变化形式，比如，Crammerand Singer提出的一种针对线性分类器的损失函数:

img

Weston and Watkins提出了一种相似定义，只不过用相加取代了求最大值：

img

        本文中所使用的Hinge损失即为上述中包含maigin的公式。
        上图即为原始Hinge损失的求导公式，为了方便计算作者为其增加了标志位（0,1,-1）用于表示两图片之间的排序关系。

Efficient Siamese backpropagation：

在反向传播阶段，对于模型参数的更新作者并未采用随机梯度下降算法而是采用了批梯度下降算法，这样一来假如我们所设置的batch-size为n那我们就可以先进行n次的正向传播完成这一batch中所有图像的处理之后再根据他们的处理结果计算hinge损失并求得均值进行反向传播。这样一来一个batch中的图片每张都只需要进行1次正向处理就可以与其余的n-1张图片完成对比，极大地降低了计算成本同时也有效保证了更新的有效性。此外在进行梯度计算时，作者采用了矩阵计算，利用GPU也极大地提升了运算效率。



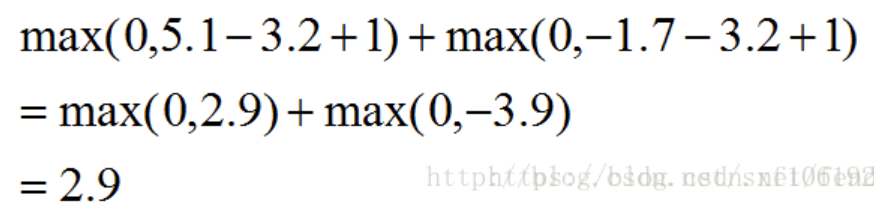
评论

发表评论

此博客中的热门博文

An overview of gradient descent optimization algorithms.

图片
  Gradient descent variants     在平时的应用过程中共有三种主流的梯度下降算法：batch gradient decent、stochastic gradient decent、mini-batch gradient decent. 其中第一种和第三种首先分别计算每一个样本的损失函数梯度之后对它们求平均作为更新依据。 Challenges Choosing a proper learning rate can be difficult.  Additionally, the same learning rate applies to all parameter updates. If our data is sparse and our features have very different frequencies, we might not want to update all of them to the same extent, but perform a larger update for rarely occurring features. Another key challenge of minimizing highly non-convex error functions common for neural networks is avoiding getting trapped in their numerous suboptimal local minima. Dauphin et al.  [3]  argue that the difficulty arises in fact not from local minima but from saddle points, i.e. points where one dimension slopes up and another slopes down. These saddle points are usually surrounded by a plateau of the same error, which makes it notoriously hard for SGD to escape, as ...
阅读全文

Visual Mechanisms Inspired Efficient Transformers for Image and Video Quality Assessment

图片
Image and video quality assessment based on swin-transformer     这是一篇2022年发表于CVPR的一篇文章，文中作者受到swin-transformer中多层注意力机制的启发，构造了一种能在多个维度层面对图像质量进行评价的图像质量评价方法。并将这一方法应用于视频片段中帧图像的质量评定。最终不论是文中提出的图像质量评定方法还是视频质量评价方法都获得了巨大的成效成为全新的标杆性方法。     在图像质量评价方面，由于使用了swin-transformer作为基础框架，作者在进行图像预处理时 对该领域所要求的高分辨率图像与swin-transformer所要求的固定分辨率图像输入中做了折中，摒弃了传统图像分类、目标检测中所做的裁剪预处理转而采用池化层对高分辨率图像的全局信息进行提取并以提取出的信息作为输入放入swin-transformer框架中进行处理。在往常的计算机视觉任务中深度学习框架往往更偏向于提取空间域或时域中的相关信息，但作者提出在图像质量评价任务中频域信息（图像中亮度/对比度的变化快慢）同样值得关注。虽然图像的频域信息在深度学习框架中很难准确地进行表示但是在每层swin-transformer的输出中各个chanel之间的相对信息可以从某种意义上展现出该图片的频域信息因此作者提出了channel attention对原有swin-transformer框架进行了改进提出了一种适用于图像质量评价的swin-transformer(multi-stage channel attention model using Swin Transformer as backbone for IQA)其框架如上图一所示。此外作者认为本文提出的这种channel attention在swin-transformer的各个层之间的注意力表现应当是近乎相同的，同时也为了减少模型的运算数据量，作者决定采用权重共享的方式为原有的swin-transformer添加channel attention机制。由于在swin-transformer各个层的输出中他们的channel数量并不相同，作者引入包含固定数量（K）的滤波器以及1×1卷积核的bottleneck卷积层对各个层的输出进行变...
阅读全文

SROCC, KROCC, PLCC, RMSE

图片
 SROCC, KROCC, PLCC, RMSE     在机器学习以及深度学习方法的学习过程中有两个指标经常被我混淆，模型的准确性以及模型的误差，其实从根本上来说这两个指标都在不同程度上描述了当前模型的优越程度，但从实际意义上来说模型误差由于参数取值，计算方式等原因并不能直接用于模型之间好坏的对比，而更偏向使用于模型的训练。与之相反，模型的准确性是人们根据特定的规则使用模型的输出计算出的一种分值，它不能直接用于模型的训练但由于其规则统一，计算方法固定。因此更加适用于模型间好坏程度的比较。本文今天所涉及的四种方法：SROCC、KROCC、PLCC以及RMSE就是应用于图像质量评价领域对相关模型进行打分的四种不同的标准。 SROCC（Spearman rank-order correlation coefficient） 当SROCC取1表示算法性能很好，-1表示很差。值越接近1，IQA算法性能越好。 KROCC（Kendall rank-order correlation coefficient） KROCC的数值越大, 说明两个数据之间的相关性越好，IQA算法性能越好；值越小说明相关性越差，IQA算法性能一般。 PLCC（Pearson’s linear correlation coefficient） PLCC 描述两组数据之间的线性相关性，其取值范围为 -1~1。当 PLCC 的值为零时，表示两组数据完全不相关（图像的客观质量分数和主观质量分数相差很大）；当 PLCC 值为 1 或 -1 时，表明两组数据完全相关（图像的客观质量分数和主观质量分数一样）。PLCC 描述算法的客观评价分与人眼主观打分之间的相关性，衡量了IQA算法预测的准确性。 参考一   参考二 RMSE（root mean square error） 均方根误差越接近于 0，IQA算法性能越好。
阅读全文