图论——网络流相关
网络流
起源:
给你一个长度为 n 的整数数组 nums 和一个整数 numSlots ,满足2 * numSlots >= n 。总共有 numSlots 个篮子,编号为 1 到 numSlots 。
你需要把所有 n 个整数分到这些篮子中,且每个篮子 至多 有 2 个整数。一种分配方案的 与和 定义为每个数与它所在篮子编号的 按位与运算 结果之和。
- 比方说,将数字
[1, 3]放入篮子1中,[4, 6]放入篮子2中,这个方案的与和为(1 AND 1) + (3 AND 1) + (4 AND 2) + (6 AND 2) = 1 + 1 + 0 + 2 = 4。
请你返回将 nums 中所有数放入 numSlots 个篮子中的最大与和。
示例 1:
输入:nums = [1,2,3,4,5,6], numSlots = 3 输出:9 解释:一个可行的方案是 [1, 4] 放入篮子 1 中,[2, 6] 放入篮子 2 中,[3, 5] 放入篮子 3 中。 最大与和为 (1 AND 1) + (4 AND 1) + (2 AND 2) + (6 AND 2) + (3 AND 3) + (5 AND 3) = 1 + 0 + 2 + 2 + 3 + 1 = 9 。
示例 2:
输入:nums = [1,3,10,4,7,1], numSlots = 9 输出:24 解释:一个可行的方案是 [1, 1] 放入篮子 1 中,[3] 放入篮子 3 中,[4] 放入篮子 4 中,[7] 放入篮子 7 中,[10] 放入篮子 9 中。 最大与和为 (1 AND 1) + (1 AND 1) + (3 AND 3) + (4 AND 4) + (7 AND 7) + (10 AND 9) = 1 + 1 + 3 + 4 + 7 + 8 = 24 。 注意,篮子 2 ,5 ,6 和 8 是空的,这是允许的。
基本概念:
网络¶
首先,请分清楚 网络(或者流网络,Flow Network)与 网络流(Flow)的概念。
网络是指一个有向图 。
每条边 都有一个权值 ,称之为容量(Capacity),当 时有 。
其中有两个特殊的点:源点(Source) 和汇点(Sink)。
流¶
设 定义在二元组 上的实数函数且满足
- 容量限制:对于每条边,流经该边的流量不得超过该边的容量,即,
- 斜对称性:每条边的流量与其相反边的流量之和为 0,即
- 流守恒性:从源点流出的流量等于汇点流入的流量,即
那么 称为网络 的流函数。对于 , 称为边的 流量, 称为边的 剩余容量。整个网络的流量为 ,即 从源点发出的所有流量之和。
一般而言也可以把网络流理解为整个图的流量。而这个流量必满足上述三个性质。
注:流函数的完整定义为
网络流的常见问题¶
网络流问题中常见的有以下三种:最大流,最小割,费用流。
最大流¶
我们有一张图,要求从源点流向汇点的最大流量(可以有很多条路到达汇点),就是我们的最大流问题。
最小费用最大流¶
最小费用最大流问题是这样的:每条边都有一个费用,代表单位流量流过这条边的开销。我们要在求出最大流的同时,要求花费的费用最小。
最小割¶
割其实就是删边的意思,当然最小割就是割掉 条边来让 跟 不互通。我们要求 条边加起来的流量总和最小。这就是最小割问题。
网络流 24 题¶
最大流¶
我们有一张图,要求从源点流向汇点的最大流量(可以有很多条路到达汇点),就是我们的最大流问题。
Ford-Fulkerson 增广路算法¶
该方法通过寻找增广路来更新最大流,有 EK,dinic,SAP,ISAP 主流算法。
求解最大流之前,我们先认识一些概念。
残量网络¶
首先我们介绍一下一条边的剩余容量 (Residual Capacity),它表示的是这条边的容量与流量之差,即 。
对于流函数 ,残存网络 (Residual Network)是网络 中所有结点 和剩余容量大于 0 的边构成的子图。形式化的定义,即 。
注意,剩余容量大于 0 的边可能不在原图 中(根据容量、剩余容量的定义以及流函数的斜对称性得到)。可以理解为,残量网络中包括了那些还剩了流量空间的边构成的图,也包括虚边(即反向边)。
增广路¶
在原图 中若一条从源点到汇点的路径上所有边的 剩余容量都大于 0,这条路被称为增广路(Augmenting Path)。
或者说,在残存网络 中,一条从源点到汇点的路径被称为增广路。如图:
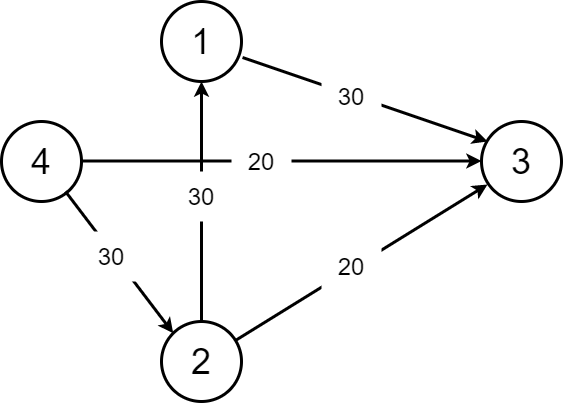
我们从 到 ,肯定可以先从流量为 的这条边先走。那么这条边就被走掉了,不能再选,总的流量为 (现在)。然后我们可以这样选择:
这条 增广路 的总流量为 。到 的时候还是 ,到 了就只有 了。
这样子我们就很好的保留了 的流量。
所以我们这张图的最大流就应该是 。
求最大流是很简单的,接下来讲解求最大流的 3 种方法。
Edmonds-Karp 动能算法(EK 算法)¶
这个算法很简单,就是 BFS 找增广路,然后对其进行 增广。你可能会问,怎么找?怎么增广?
找?我们就从源点一直 BFS 走来走去,碰到汇点就停,然后增广(每一条路都要增广)。我们在 BFS 的时候就注意一下流量合不合法就可以了。
增广?其实就是按照我们找的增广路在重新走一遍。走的时候把这条路的能够成的最大流量减一减,然后给答案加上最小流量就可以了。
再讲一下 反向边。增广的时候要注意建造反向边,原因是这条路不一定是最优的,这样子程序可以进行反悔。假如我们对这条路进行增广了,那么其中的每一条边的反向边的流量就是它的流量。
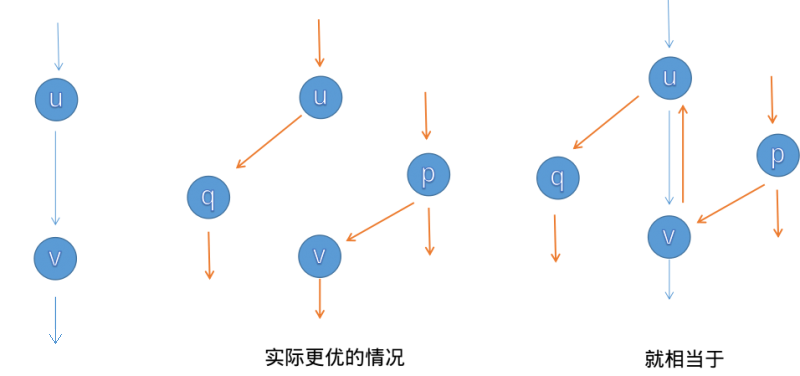
讲一下一些小细节。如果你是用邻接矩阵的话,反向边直接就是从 变成 。如果是常用的链式前向星,那么在加入边的时候就要先加入反向边。那么在用的时候呢,我们直接 就可以了 ( 为边的编号)。为什么呢?相信大家都是知道 的,那么我们在加入正向边后加入反向边,就是靠近的,所以可以使用 。我们还要注意一开始的编号要设置为 ,因为边要从编号 开始,这样子 对编号 的边才有效果。
EK 算法的时间复杂度为 (其中 为点数, 为边数)。效率还有很大提升空间。
Dinic 算法¶
Dinic 算法 的过程是这样的:每次增广前,我们先用 BFS 来将图分层。设源点的层数为 ,那么一个点的层数便是它离源点的最近距离。
通过分层,我们可以干两件事情:
- 如果不存在到汇点的增广路(即汇点的层数不存在),我们即可停止增广。
- 确保我们找到的增广路是最短的。(原因见下文)
接下来是 DFS 找增广路的过程。
我们每次找增广路的时候,都只找比当前点层数多 的点进行增广(这样就可以确保我们找到的增广路是最短的)。
Dinic 算法有两个优化:
- 多路增广:每次找到一条增广路的时候,如果残余流量没有用完怎么办呢?我们可以利用残余部分流量,再找出一条增广路。这样就可以在一次 DFS 中找出多条增广路,大大提高了算法的效率。
- 当前弧优化:如果一条边已经被增广过,那么它就没有可能被增广第二次。那么,我们下一次进行增广的时候,就可以不必再走那些已经被增广过的边。
时间复杂度¶
设点数为 ,边数为 ,那么 Dinic 算法的时间复杂度(在应用上面两个优化的前提下)是 ,在稀疏图上效率和 EK 算法相当,但在稠密图上效率要比 EK 算法高很多。
首先考虑单轮增广的过程。在应用了 当前弧优化 的前提下,对于每个点,我们维护下一条可以增广的边,而当前弧最多变化 次,从而单轮增广的最坏时间复杂度为 。
接下来我们证明,最多只需 轮增广即可得到最大流。
我们先回顾下 Dinic 的增广过程。对于每个点,Dinic 只会找比该点层数多 的点进行增广。
首先容易发现,对于图上的每个点,一轮增广后其层数一定不会减小。而对于汇点 ,情况会特殊一些,其层数在一轮增广后一定增大。
对于后者,我们考虑用反证法证明。如果 的层数在一轮增广后不变,则意味着在上一次增广中,仍然存在着一条从 到 的增广路,且该增广路上相邻两点间的层数差为 。这条增广路应该在上一次增广过程中就被增广了,这就出现了矛盾。
从而我们证明了汇点的层数在一轮增广后一定增大,即增广过程最多进行 次。
综上 Dinic 的最坏时间复杂度为 。事实上在一般的网络上,Dinic 算法往往达不到这个上界。
特别地,在求解二分图最大匹配问题时,Dinic 算法的时间复杂度是 。接下来我们将给出证明。
首先我们来简单归纳下求解二分图最大匹配问题时,建立的网络的特点。我们发现这个网络中,所有边的流量均为 ,且除了源点和汇点外的所有点,都满足入边最多只有一条,或出边最多只有一条。我们称这样的网络为 单位网络。
对于单位网络,一轮增广的时间复杂度为 ,因为每条边只会被考虑最多一次。
接下来我们试着求出增广轮数的上界。假设我们已经先完成了前 轮增广,因为汇点的层数在每次增广后均严格增加,因此所有长度不超过 的增广路都已经在之前的增广过程中被增广。设前 轮增广后,网络的流量为 ,而整个网络的最大流为 ,设两者间的差值 。
因为网络上所有边的流量均为 ,所以我们还需要找到 条增广路才能找到网络最大流。又因为单位网络的特点,这些增广路不会在源点和汇点以外的点相交。因此这些增广路至少经过了 个点(每条增广路的长度至少为 ),且不能超过 个点。因此残量网络上最多还存在 条增广路。也即最多还需增广 轮。
综上,对于包含二分图最大匹配在内的单位网络,Dinic 算法可以在 的时间内求出其最大流。
MPM 算法¶
MPM(Malhotra, Pramodh-Kumar and Maheshwari) 算法得到最大流的方式有两种:使用基于堆的优先队列,时间复杂度为 ;常用 BFS 解法,时间复杂度为 。注意,本章节只专注于分析更优也更简洁的 算法。
MPM 算法的整体结构和 Dinic 算法类似,也是分阶段运行的。在每个阶段,在 的残量网络的分层网络中找到增广路。它与 Dinic 算法的主要区别在于寻找增广路的方式不同:MPM 算法中寻找增广路的部分的只花了 , 时间复杂度要优于 Dinic 算法。
MPM 算法需要考虑顶点而不是边的容量。在分层网络 中,如果定义点 的容量 为其传入残量和传出残量的最小值,则有:
我们称节点 是参考节点当且仅当 。对于一个参考节点 ,我们一定可以让经过 的流量增加 以使其容量变为 。这是因为 是有向无环图且 中节点容量至少为 ,所以我们一定能找到一条从 经过 到达 的有向路径。那么我们让这条路上的边流量都增加 即可。这条路即为这一阶段的增广路。寻找增广路可以用 BFS。增广完之后所有满流边都可以从 中删除,因为它们不会在此阶段后被使用。同样,所有与 和 不同且没有出边或入边的节点都可以删除。
时间复杂度分析¶
MPM 算法的每个阶段都需要 ,因为最多有 次迭代(因为至少删除了所选的参考节点),并且在每次迭代中,我们删除除最多 之外经过的所有边。求和,我们得到 。由于阶段总数少于 ,因此 MPM 算法的总运行时间为 。
阶段总数小于 V 的证明¶
MPM 算法在少于 个阶段内结束。为了证明这一点,我们必须首先证明两个引理。
引理 1:每次迭代后,从 到每个点的距离不会减少,也就是说,。
证明:固定一个阶段 和点 。考虑 中从 到 的任意最短路径 。 的长度等于 。注意 只能包含 的后向边和前向边。如果 没有 的后边,那么 。因为 也是 中的一条路径。现在,假设 至少有一个后向边且第一个这样的边是 ,那么 (因为第一种情况)。边 不属于 ,因此 受到前一次迭代的增广路的影响。这意味着 。此外,。从这两个方程和 我们得到 。路径的剩余部分也可以使用相同思想。
引理 2:。
证明:从引理一我们得出,。假设 ,注意 只能包含 的后向边和前向边。这意味着 中有一条最短路径未被增广路阻塞。这就形成了矛盾。
ISAP¶
在 Dinic 算法中,我们每次求完增广路后都要跑 BFS 来分层,有没有更高效的方法呢?
答案就是下面要介绍的 ISAP 算法。
和 Dinic 算法一样,我们还是先跑 BFS 对图上的点进行分层,不过与 Dinic 略有不同的是,我们选择在反图上,从 点向 点进行 BFS。
执行完分层过程后,我们通过 DFS 来找增广路。
增广的过程和 Dinic 类似,我们只选择比当前点层数少 的点来增广。
与 Dinic 不同的是,我们并不会重跑 BFS 来对图上的点重新分层,而是在增广的过程中就完成重分层过程。
具体来说,设 号点的层为 ,当我们结束在 号点的增广过程后,我们遍历残量网络上 的所有出边,找到层最小的出点 ,随后令 。特别地,若残量网络上 无出边,则 。
容易发现,当 时,图上不存在增广路,此时即可终止算法。
和 Dinic 类似,ISAP 中也存在 当前弧优化。
而 ISAP 还存在另外一个优化,我们记录层数为 的点的数量 ,每当将一个点的层数从 更新到 时,同时更新 数组的值,若在更新后 ,则意味着图上出现了断层,无法再找到增广路,此时可以直接终止算法(实现时直接将 标为 ),该优化被称为 GAP 优化。
Push-Relabel 预流推进算法¶
该方法在求解过程中忽略流守恒性,并每次对一个结点更新信息,以求解最大流。
通用的预流推进算法¶
首先我们介绍预流推进算法的主要思想,以及一个可行的暴力实现算法。
预流推进算法通过对单个结点的更新操作,直到没有结点需要更新来求解最大流。
算法过程维护的流函数不一定保持流守恒性,对于一个结点,我们允许进入结点的流超过流出结点的流,超过的部分被称为结点 的 超额流 :
若 ,称结点 溢出4,注意当我们提到溢出结点时,并不包括 和 。
预流推进算法维护每个结点的高度 ,并且规定溢出的结点 如果要推送超额流,只能向高度小于 的结点推送;如果 没有相邻的高度小于 的结点,就修改 的高度(重贴标签)。
高度函数5¶
准确地说,预流推进维护以下的一个映射 :
称 是残存网络 的高度函数。
引理 1:设 上的高度函数为 ,对于任意两个结点 ,如果 ,则 不是 中的边。
算法只会在 的边执行推送。
推送(Push)¶
适用条件:结点 溢出,且存在结点 ,则 push 操作适用于 。
于是,我们尽可能将超额流从 推送到 ,推送过程中我们只关心超额流和 的最小值,不关心 是否溢出。
如果 在推送完之后满流,将其从残存网络中删除。
重贴标签(Relabel)¶
适用条件:如果结点 溢出,且 ,则 relabel 操作适用于 。
则将 更新为 即可。
初始化¶
上述将 充满流,并将 抬高,使得 ,因为 ,而且 毕竟满流,没必要留在残存网络中;上述还将 初始化为 的相反数。
通用算法¶
我们每次扫描整个图,只要存在结点 满足 push 或 relabel 操作的条件,就执行对应的操作。
如图,每个结点中间表示编号,左下表示高度值 ,右下表示超额流 ,结点颜色的深度也表示结点的高度;边权表示 ,绿色的边表示满足 的边 (即残存网络的边 ):
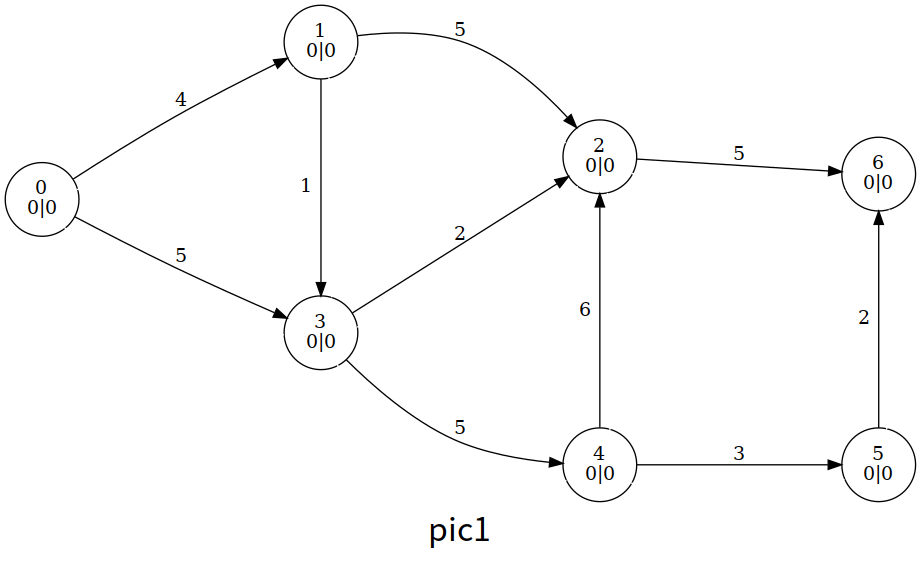
整个算法我们大致浏览一下过程,这里笔者使用的是一个暴力算法,即暴力扫描是否有溢出的结点,有就更新
最后的结果
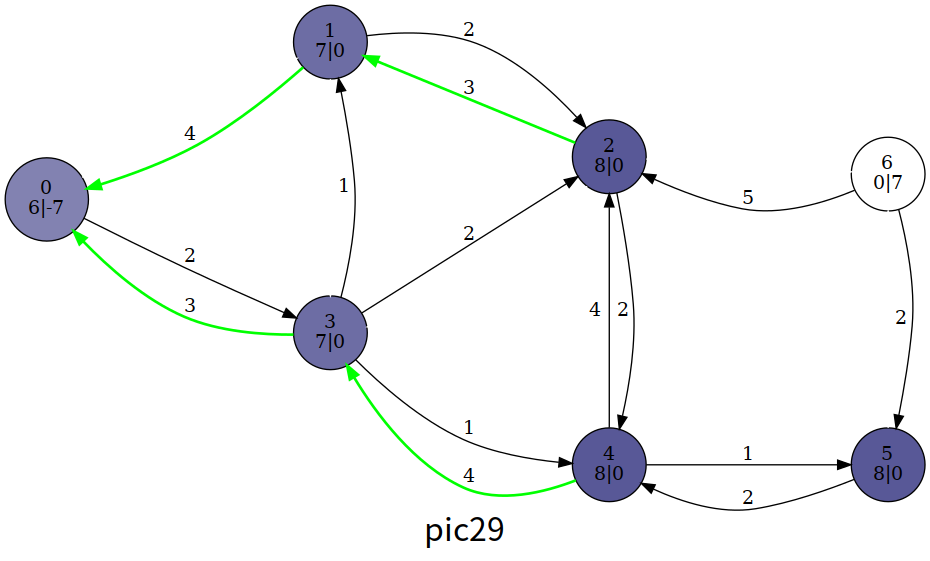
可以发现,最后的超额流一部分回到了 ,且除了源点汇点,其他结点都没有溢出;这时的流函数 满足流守恒性,为最大流,流量即为 。
但是实际上论文1指出只处理高度小于 的溢出节点也能获得正确的最大流值,不过这样一来算法结束的时候预流还不满足流函数性质,不能知道每条边上真实的流量。
最小割
割¶
对于一个网络流图 ,其割的定义为一种 点的划分方式:将所有的点划分为 和 两个集合,其中源点 ,汇点 。
割的容量¶
我们的定义割 的容量 表示所有从 到 的边的容量之和,即 。当然我们也可以用 表示 。
最小割¶
最小割就是求得一个割 使得割的容量 最小。
证明¶
最大流最小割定理¶
定理:
对于任意一个可行流 的割 ,我们可以得到:
如果我们求出了最大流 ,那么残余网络中一定不存在 到 的增广路经,也就是 的出边一定是满流, 的入边一定是零流,于是有:
结合前面的不等式,我们可以知道此时 已经达到最大。
费用流¶
给定一个网络 ,每条边除了有容量限制 ,还有一个单位流量的费用 。
当 的流量为 时,需要花费 的费用。
也满足斜对称性,即 。
则该网络中总花费最小的最大流称为 最小费用最大流,即在最大化 的前提下最小化 。
SSP 算法¶
SSP(Successive Shortest Path)算法是一个贪心的算法。它的思路是每次寻找单位费用最小的增广路进行增广,直到图上不存在增广路为止。
如果图上存在单位费用为负的圈,SSP 算法正确无法求出该网络的最小费用最大流。此时需要先使用消圈算法消去图上的负圈。
证明¶
我们考虑使用数学归纳法和反证法来证明 SSP 算法的正确性。
设流量为 的时候最小费用为 。我们假设最初的网络上 没有负圈,这种情况下 。
假设用 SSP 算法求出的 是最小费用,我们在 的基础上,找到一条最短的增广路,从而求出 。这时 是这条最短增广路的长度。
假设存在更小的 ,设它为 。因为 已经是最短增广路了,所以 一定对应一个经过 至少一个负圈 的增广路。
这时候矛盾就出现了:既然存在一条经过至少一个负圈的增广路,那么 就不是最小费用了。因为只要给这个负圈添加流量,就可以在不增加 流出的流量的前提下,使 对应的费用更小。
综上,SSP 算法可以正确求出无负圈网络的最小费用最大流。
时间复杂度¶
如果使用 Bellman-Ford 算法 求解最短路,每次找增广路的时间复杂度为 。设该网络的最大流为 ,则最坏时间复杂度为 。事实上,SSP 算法是 伪多项式时间 的。
SSP 算法的时间复杂度有 的上界,这是一个关于值域的多项式,所以是伪多项式时间的。
可以构造 的网络1使得 SSP 算法的时间复杂度达到 ,所以 SSP 算法不是多项式时间的。
实现¶
只需将 EK 算法或 Dinic 算法中找增广路的过程,替换为用最短路算法寻找单位费用最小的增广路即可。
Primal-Dual 原始对偶算法¶
用 Bellman-Ford 求解最短路的时间复杂度为 ,无论在稀疏图上还是稠密图上都不及 Dijkstra 算法2。但网络上存在单位费用为负的边,因此无法直接使用 Dijkstra 算法。
Primal-Dual 原始对偶算法的思路与 Johnson 全源最短路径算法 类似,通过为每个点设置一个势能,将网络上所有边的费用(下面简称为边权)全部变为非负值,从而可以应用 Dijkstra 算法找出网络上单位费用最小的增广路。
首先跑一次最短路,求出源点到每个点的最短距离(也是该点的初始势能)。接下来和 Johnson 算法一样,对于一条从 到 ,单位费用为 的边,将其边权重置为 。
可以发现,这样设置势能后新网络上的最短路径和原网络上的最短路径一定对应。证明在介绍 Johnson 算法时已经给出,这里不再展开。
与常规的最短路问题不同的是,每次增广后图的形态会发生变化,这种情况下各点的势能需要更新。
如何更新呢?先给出结论,设增广后从源点到 号点的最短距离为 (这里的距离为重置每条边边权后得到的距离),只需给 加上 即可。下面我们证明,这样更新边权后,图上所有边的边权均为非负。
容易发现,在一轮增广后,由于一些 边在增广路上,残量网络上会相应多出一些 边,且一定会满足 (否则 边就不会在增广路上了)。稍作变形后可以得到 。因此新增的边的边权非负。
而对于原有的边,在增广前,,因此 ,即用 作为新势能并不会使 的边权变为负。
综上,增广后所有边的边权均非负,使用 Dijkstra 算法可以正确求出图上的最短路。


评论
发表评论